Krystyna Burczyk's Origami Gallery - regular polyhedra

Polyhedra classification

Regular polyhedra have identical faces and identical vertices. Additionally every face is a regular polygon and every vertex is regular. There are five regular polyhedra, also called Platonic solids: tetrahedron (triangle faces, 3 in each vertex), hexahedron or cube (square faces, 3 in each vertex), octahedron (triangle faces, 4 in each vertex), dodecahedron (pentagonal faces, 3 in each vertex), icosahedron (triangle faces, 5 in each vertex).

Semi-regular polyhedra have identical vertices. Additionally every face is a regular polygon. The semi-regular polyhedra are also called Archimedean solids.

Every regular and semi-regular polyhedron is described by its vertex index. The index is a sequence of integers. Each of them denotes the number of sides of a face in this vertex. For example (4, 6, 6) is the index of a polyhedron with vertices of degree 3 - one square and two hexagons join in each vertex to form a truncated octahedron.

There are great polyhedra pages by Roman E. Maeder at ETH in Zurich (http://www.mathconsult.ch/showroom/unipoly/index.html) and George W. Hart (http://www.georgehart.com).

Regular polyhedra models (Platonic solids)

Tetrahedron 4 vertices, 6 edges, 4 faces (regular triangles), index (3, 3, 3)
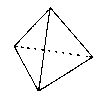
Cube (hexahedron) 8 vertices, 12 edges, 6 faces (squares), index (4, 4, 4)
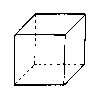
Octahedron 6 vertices, 12 edges, 8 faces (regular triangles), index (3, 3, 3, 3)
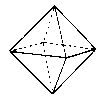
Dodecahedron 20 vertices, 30 edges, 12 faces (regular pentagons), index (5, 5, 5)
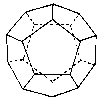
Icosahedron 12 vertices, 30 edges, 20 faces (regular triangles), index (3, 3, 3, 3, 3)

Semi-regular polyhedra models (Archimedean solids)

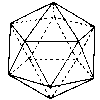
Truncated tetrahedron 12 vertices, 18 edges, 8 faces (4 regular triangles, 4 regular hexagons), index (3, 6, 6)

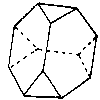
Truncated cube 24 vertices, 36 edges, 14 faces (8 regular triangles, 6 regular octagons), index (3, 8, 8)
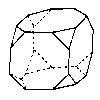
Cubooctahedron 12 vertices, 24 edges, 14 faces (8 regular triangles, 6 squares), index (3, 4, 3, 4)
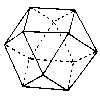
Truncated octahedron 24 vertices, 36 edges, 14 faces (6 squares, 8 regular hexagons), index (4, 6, 6)
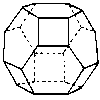
Snub cube 24 vertices, 60 edges, 38 faces (32 regular triangles, 6 squares), index (3, 3, 3, 3, 4). There are two variations of snub cube: left-handed and right-handed.
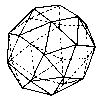
Lesser rhombicubooctahedron 24 vertices, 48 edges, 26 faces (8 regular triangles, 18 squares), index (3, 4, 4, 4).
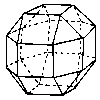
Greater rhombicubooctahedron 48 vertices, 72 edges, 26 faces (12 squares, 8 regular hexagons, 6 regular octagons), index (4, 6, 8).
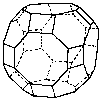
Truncated dodecahedron 60 vertices, 90 edges, 32 faces (20 regular triangles, 12 regular decagons), index (3, 10, 10).
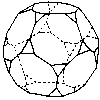
Icosidodecahedron 30 vertices, 60 edges, 32 faces (20 regular triangles, 12 regular pentagons), index (3, 5, 3, 5).
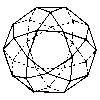
Truncated icosahedron 60 vertices, 90 edges, 32 faces (12 regular pentagons, 20 regular hexagons), index (5, 6, 6).
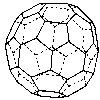
Snub dodecahedron 60 vertices, 150 edges, 92 faces (80 regular triangles, 12 regular pentagons), index (3, 3, 3, 3, 5). There are two variations of snub dodecahedron: left-handed and right-handed.
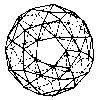
Lesser rhombicosidodecahedron 60 vertices, 120 edges, 62 faces (20 regular triangles, 30 squares, 12 regular pentagons), index (3, 4, 5, 4).
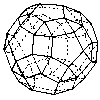
Great rhombicosidodecahedron 120 vertices, 180 edges, 62 faces (30 squares, 20 regular hexagons, 12 regular decagons), index (4, 10, 6).


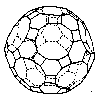
Previous	Home	Up	Map	po polsku	Next