



Tomoko Fuse's edge unit (open frame 2) is my favourite unit for polyhedra construction. Unfortunatelly there is shortcoming. It is not possible to obtain an angle greater than right angle between two edges in model build using these modules. As a consequence, you can easy obtain only equilateral triangle and square. To build polyhedra models you need also pentagons, hexagons, octagons and dodecagons. It is relatively easy to obtain a pentagon or a hexagon - simply add "spokes" as you can see on picture below. It is nor so easy to obtain polygon with larger number of sides - you must build more sofisticated construction.
We start with triangle, square or pentagon. Then we duplicate sides to obtain regular hexagon, octagon or decagon. To duplicate sides we can use triangles or square. In the first case a resulting dome is more flat and it requires less modules (the lesser dome). In the later case a resulting dome is higher, very stable, but it requires more modules (the greater dome).
We can also use units of various lengths instead of construction of domes. However the way described here is easier at stage of unit folding (all uniform) and gives very nice results.
Following schemes do not preserve length. They also are not the projection of domes. They are graphs. In fact every edge has the same length. The graph is similar to electricity schema - it shows connections not lengths. Every colored edge is horizontal, the black one is skew.
| Lesser domes | Greater domes | |
| The simplest case - pentagon. To obtain a pentagen we add spokes. To form nice pentagon, the spokes should be let inside model. |
|
|
| We can do the same with hexagon - the obtained face is flat. |
|
|
| The lesser dome is low. The grater dome is high. The construction of the greater dome can be extended. After building the next two levels we can obtain dodecagon. |
|
|
|
The octagon dome is built on square. We build next square at each side and join them with triangles. Then we obtain a lesser dome. It is not so high.
To obtain a greater dome we start with a square.
Then we add additional three edges at each square corner.
When we join free ends by edges, the first level is ready - we have obtained a square with side lenght 2.
|
|
|
|
The decagon dome is built on pentagon with spokes. We build a square at each side of pentagon and join them with triangles. Then we obtain a lesser dome. It's low and can be all cupped. It is also not so stiff and it tend to deformation.
To obtain a greater dome we start with a pentagon with spokes.
Then we add additional three edges at each pentagon corner.
When we join free ends by edges, the first level is ready - we have obtained a pentagon with side lenght 2.
|
|
|
You can obtain the most showy models with domes if you build domes on truncated polyhedra.
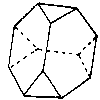
|

|
|
|
| ||
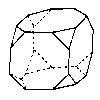
|

|
|
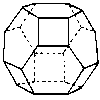
|

|
|
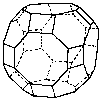
|

|
|
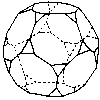
|

|
|
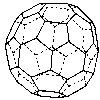
|

|
|
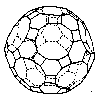
|

|
|
|
|
|
|
|
|
| Previous | Home | Up | Map | po polsku | Next |